Vitesse de libération

La vitesse de libération correspond à la vitesse minimale qu'un objet doit avoir pour s'éloigner à l'infini de l'astre malgré l'attraction gravitationnelle.

Pour son calcul, j'utiliserai les variables : - M, masse de l'astre - m, masse de l'objet - R, rayon de l'astre - r, distance entre l'astre et l'objet - F, la force d'attraction à la distance r tel que F = GMm/r²

On cherche maintenant le travail à fournir pour déplacer l'objet de r=R à r=∞ en s'opposant à la gravité. Or, on sait que le travail est égal à la force multiplié par la distance. Ici la force n'est pas constante, il faut donc intégrer.

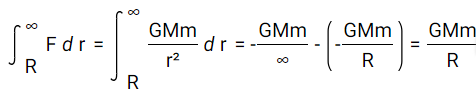
Ce travail doit donc être fourni uniquement par la vitesse de l'objet, plus exactement son énergie cinétique. On pose alors l'égalité :

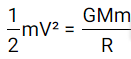
Ainsi, V correspond à la vitesse de libération. On l'isole dans la formule précédente pour obtenir :

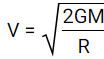
On remarque que cette vitesse ne dépend pas de la masse de l'objet mais uniquement des caractéristiques de l'astre, elle est donc propre à l'astre.

Trous noirs

Par définition, un trou noir est un astre si massif et dense que même la lumière ne peut s'en échapper malgré sa vitesse de 3E8 m/s. La vitesse de libération d'un trou noir est égale à celle de la lumière. En réutilisant les résultats de la partie précédente, on peut retrouver la formule du rayon de Schwarzschild qui permet de calculer le rayon d'un trou noir selon sa masse.

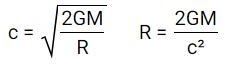
On remarque que la densité globale des trous noirs est variable car la masse augmente linéairement avec le rayon et non au cube, ainsi plus un trou noir est grand, moins il est dense. Sa masse volumique peut être exprimée tel que :

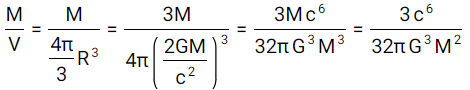
Par exemple un trou noir d'environ 2.7E38 kg aurait la densité globale de l'eau. Mais la densité n'est pas homogène dans un trou noir, le centre subit plus de contraintes et est donc plus compact.