Dans cet article, je vais présenter une méthode pour modifier les composantes d'un vecteur pour lui appliquer une rotation.

Réprésentation polaire d'un vecteur

Dans un repère en deux dimensions, on représente habituellement un vecteur par ces deux composantes. Mais pour résoudre ce problème, il est plus pratique d'utiliser une représentation polaire avec les deux paramètres que sont la norme r et l'angle θ formé entre l'axe des abscisses et le vecteur.

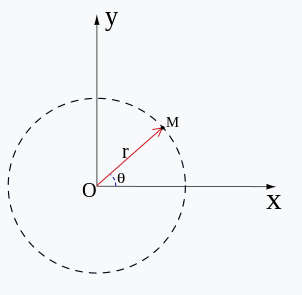
On peut faire le passage entre les deux systèmes avec : x = r*cos(θ) et y = r*sin(θ). Ainsi, pour appliquer une rotation de paramètre a à un vecteur u de paramètres r et θ, il suffit de calculer le vecteur u' de paramètres r et θ + a. Les nouvelles coordonnées deviennent donc : x' = r*cos(θ + a) et y' = r*cos(θ + a). On peut ensuite utiliser les formules d'additions trigonométriques. x' = r*(cos(θ)*cos(a)-sin(θ)*sin(a)) = r*cos(θ)*cos(a) - r*sin(θ)*sin(a) et y' = r*(cos(θ)*sin(a) + sin(θ)*cos(a)) = r*cos(θ)*sin(a) + r*sin(θ)*cos(a).

Utilisation des matrices

Dans l'expression des coordonnées de u', on retrouve les coordonnées de u, on peut donc écrire : x' = x*cos(a) - y*sin(a) et y' = x*sin(a) + y*cos(a). On peut remarquer que ces opérations peuvent être effectuer par un produit matriciel tel que :

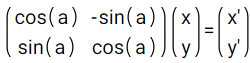
La matrice carrée à droite est dite de rotation, elle dépend d'un paramètre d'angle a. Il suffit donc de la multiplier par le vecteur à tourner pour obtenir le nouveau vecteur.