Dans cet article je vais présenter deux manières de calculer l'intégrale suivante :

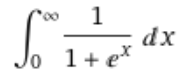
Première méthode

La première fois que je l'ai résolue, j'ai utilisé une succession de changements de variable, ce qui rend la résolution relativement longue.

Le premier est : x = 2t , donc dx = 2dt et les bornes ne changent pas. De plus, on peut sortir le facteur 2 de l'exponentielle et en faire un carré.

Ce changement de variable sert à se rapprocher d'une forme 1/(1+x²) qui peut être aisément résolue par un changement de variable tel que x = tan(u). Ainsi dx = 1+tan(u)² du , le numérateur et le dénominateur s'annule, il ne reste plus qu'à intégrer du.

On procède donc au second changement de variable qui vise à transformer exp(t) en tan(u). On pose donc t = ln(tan(u)) et dt = (1+tan(u)²)/tan(u) du. il faut ensuite changer les bornes d'intégrations. En remaniant l'expression de t on obtient : u = arctan(exp(t)), la borne inférieure devient donc arctan(exp(0)) = arctan(1) = π/4 et la supérieure devient :

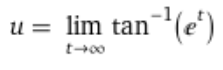
Or l'exponentielle tend vers l'infini et l'arctangente tend vers π/2 en l'infini, la borne supérieure est donc π/2. Après remplacement, on obtient:

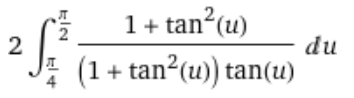
Que l'on peut simplifier par:

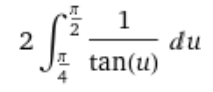
Ensuite, on réécrit la tangente sous sa forme sin(u)/cos(u).

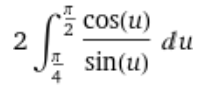
Or, le cosinus est la dérivée du sinus, on a donc une forme v'/v dont une primitive est ln(v). Cette intégrale est donc égale à deux fois l'évaluation de ln(sin(u)) de π/4 à π/2, soit 2 * (ln(sin(π/2)) - ln(sin(π/4))) = 2 * (ln(1) - ln(√2/2)) = 2 * (0 + ln(2/√2)) = 2*ln(√2) = ln(2).

Notre intégrale de départ vaut donc ln(2).

Deuxième méthode

Pour cette deuxième méthode, nous allons profiter de la linéarité de l'intégrale pour la transformer en une seconde intégrale plus simple.

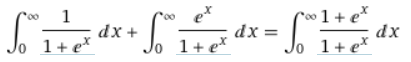
On isole ensuite la sigmoïde.

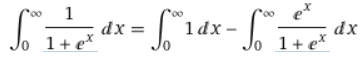
L'intégration de dx ne pose pas de problème si ce n'est que la borne supérieure est l'infini faisant donc tendre l'intégrale vers l'infini. Mais concentrons-nous d'abord sur la deuxième intégrale. Celle-ci est de forme v'/v car exp(x) est la dérivée de exp(x) + 1, une primitive est donc ln(exp(x) + 1). L'intégration de la sigmoïde devient donc l'évaluation de x - ln(exp(x) + 1) de 0 à l'infini, soit L = lim x - 0 - ln(exp(x) + 1) + ln(exp(0) + 1) = lim x - ln(exp(x) + 1) + ln(2). On peut réécrire x comme ln(exp(x)). Or la limite en l'infini de exp(x) et de exp(x) + 1 sont les mêmes d'après la règle de l'hôpital, ainsi ln(exp(x)) et ln(exp(x) + 1) s'annule et il ne reste que ln(2). On retrouve la même valeur et bien plus rapidement.