Quel rapport peut-il y avoir entre l'analyse complexe et les nombres premiers ? A priori, il semblerait que les deux domaines n'aient pas de lien évident. Pourtant, en 1859, Riemann introduit dans un article une nouvelle fonction qui permet de matérialiser ce lien. Cette fonction analytique, nommée fonction zêta, est définie pour un complexe s tel que :

En multipliant successivement par le deuxième terme de la somme et en soustrayant le résultat à la première expression, on supprime tous les termes de la somme comportant un multiple de ce nombre premier. Les premières itérations sont formalisées ci-dessous :
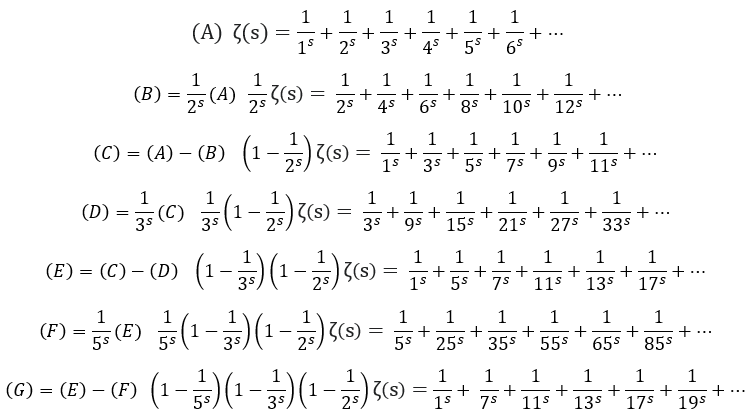
En continuant ce raisonnement indéfiniment, la fonction se comporte comme un crible d'Eratosthène. Elle supprime les multiples dans le membre de droite et isole les nombres premiers dans celui de gauche. On retrouve ainsi le produit eulérien :
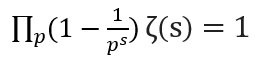
La fonction zêta crée donc un pont entre l'analyse complexe et l'arithmétique. Ses zéros donnent de cette manière des informations sur la répartition des nombres premiers, qui est encore à ce jour un mystère des mathématiques.